Question

Which choice is equivalent to the quotient shown here for acceptable values of x?

Answer 1

Choice D

Explanation:

The division of the two radicals can be re-written in the following format;

`\frac{√(30(x-1)) }{\sqrt{5(x-1)^(2) } }`

Using the properties of radicals division, the expression can further be written as;

`\sqrt{(30(x-1))/(5(x-1)^(2) ) }`

We simplify the terms under the radical sign to obtain;

`\sqrt{(6)/(x-1) }`

Choice D is thus the correct solution

Answer 2

Answer: OPTION D

Explanation:

You need to remember this property:

`(√(x) )/(√(y) )=\sqrt{(x)/(y) }`

And remember that:

`(a)/(a)=1`

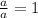
Then, the first step is rewrite the expression:

`(√(30(x-1)) )/(√(5(x-1)^2))`
`=\sqrt{(30(x-1))/(5(x-1)^2)} }`

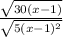
Now, to find the corresponding equivalent expression, you need to simplify the expression.

Therefore, the equivalent expression is the following:

`\sqrt{(6)/((x-1))} }`

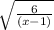
Finally, you can observe that this matches with the option D.