Answer: I and II.
Explanation:
By definition, two solids are similar if their corresponding sides are in the same ratio.
Knowing this, let's find which solids are similar:
Corresponding sides ratio of solids I and II:
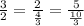
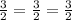
Corresponding sides ratio of solids I and III:
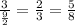
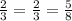
Corresponding sides ratio of solids II and III:
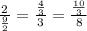
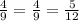
You can observe that the solids I and II are similar.