Question

Suppose that you are standing on a train accelerating at 0.39g. What minimum coefficient of static friction must exist between your feet and the floor if you are not to slide?

Static friction is the friction that exist between a stationary object and the surface on which it is resting. Coefficient of friction tells us how strongly the two surfaces grip each other. Static friction and coefficient of friction are related to each other by the relation;

Fs=μsN

where,

Fs=Force of static friction
μs=Coefficient of friction
N=Normal force

Answer 1

0.39

Step-by-step explanation:

In order not to slide, you must have exactly the same acceleration of the train:

`a=0.39 g`

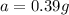
where

g = 9.81 m/s^2

There is only one force acting on you: the static frictional force that "pulls" you forward, and it is given by

`F_s = \mu_s mg`

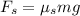
According to Newton's second law, the net force acting on you (so, the frictional force) must be equal to your mass times the acceleration, so we have

`F= ma = \mu_s mg`

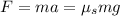
from which we find

`\mu_s = (a)/(g)=(0.39 g)/(g)=0.39`

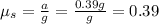
so, the minimum coefficient of static friction must be 0.39.