Question

When a fixed amount of ideal gas goes through an isobaric expansion

Question 21 options:

the gas does no work.

no heat enters or leaves the gas.

its internal (thermal) energy does not change.

its temperature must increase.

its pressure must increase.

Answer 1

its temperature must increase.

Step-by-step explanation:

An isobaric expansion is a transformation in which the pressure of the gas does not change (isobaric), while the volume increases (expansion).

Since the pressure does not change,

"its pressure must increase."

is a false statement.

The 1st law of thermodynamics is

`\Delta U = Q - W`

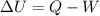
where

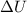`\Delta U` is the change in internal energy of the gas, which is proportional to the change in temperature:
`\Delta U \propto \Delta T`

Q is the heat supplied to the gas

W is the work done by the gas, which is given by

`W=p\Delta V`

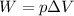
where p is the pressure and
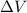`\Delta V` is the change in volume. Since the gas is expanding, we can say that
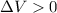`\Delta V>0`, so the gas does positive work:

`W>0`

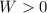
This means that the option

"the gas does no work."

is false.

Moreover, from the ideal gas law

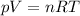`pV=nRT` (2)

we also know that the temperature of the gas is increasing (because p, the pressure, n the number of moles, and R, the gas constant, are all constant in this process, and since the volume V is increasing, than the temperature T must be increasing also)

So, we know that the option

"its internal (thermal) energy does not change. "

is false.

Finally, in an isobaric expansion, in order to keep the pressure constant heat should be supplied to the system, so

"no heat enters or leaves the gas."

is also wrong

We also said from (2) that the temperature of the gas is increasing, therefore the statement

"its temperature must increase."

is the only correct one.