Question

Find any points of discontinuity for y=x^2/x^2+1

Answer 1

The function is continuous for all real numbers

Explanation:

We have the following function

`y=(x^2)/(x^2+1)`

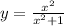
Note that the denominator of the function is:

`x^2 +1`

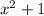
This expression is different from zero for all real numbers, since for
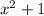`x^2 +1` then
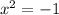`x^2 =-1`, there is no number in the real numbers whose square root is equal to -1.

For this reason the function is defined for all real numbers and has no discontinuity.

This function is always positive, continuous and has horizontal asymptote

`y = 1`

Observe the attached image