Question

Line m is parallel to line n. The measure of angle 4 is (5a + 10)°. The measure of angle 6 is (3a + 10)°. What is the measure of angle 4?

A. 110°
B. 70°
C. 20°
D. 60°

Answer 1

A. 110

Explanation:

Angles 4 and 6 are supplementary so if we add them together they will equal 180.

(5a + 10)° + (3a + 10)° = 180°

Simplify a bit to get 8a + 20 = 180

and 8a = 160.

a = 20. Now sub that value of a into the expression for angle 4:

5a + 10 --> 5(20) + 10 = 110°

Answer 2

Option A.

Explanation:

Given information: m║n,
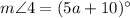`m\angle 4=(5a+10)^(\circ)` and
`m\angle 6=(3a+10)^(\circ)`.

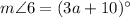If a transversal line intersect two parallel lines, then the interior angles on the same sides are supplementary angles. It means their sum is 180.

From the given figure it is clear that angle 4 angle 6 are interior angles on the same side. So, angle 4 and 6 are supplementary angles.

`m\angle 4+m\angle 6=180^(\circ)`

`(5a+10)+(3a+10)=180`

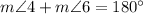
On combining like terms we get

`(5a+3a)+(10+10)=180`

`8a+20=180`

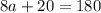
Subtract 20 from both sides.

`8a+20-20=180-20`

`8a=160`

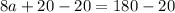
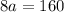
Divide both sides by 8.

`a=20`

The value of a is 20.

`m\angle 4=(5a+10)^(\circ)\Rightarrow 5(20)+10)^(\circ)=110^(\circ)`

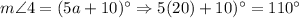
Therefore, the correct option is A.