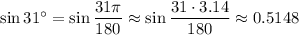For this question, you could have estimated

so that you would expect about

In general, computing
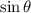 (
(
 in radians) by hand is tedious and difficult, but there are several ways to do it. Calculutors typically use well-known approximations in the form of truncated series expansions, such as
in radians) by hand is tedious and difficult, but there are several ways to do it. Calculutors typically use well-known approximations in the form of truncated series expansions, such as
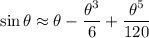
Then