Question

In school 40% of the students play tennis, 24% of the students play baseball, and 58% of the students playing neither tennis or baseball, if you pick a student at random what is the probability that the student plays both tennis and baseball

Answer 1

Answer: The required probability that the random student selected plays both tennis and basketball is 22%.

Step-by-step explanation: Given that in a school, 40% of the students play tennis, 24% of the students play baseball, and 58% of the students playing neither tennis or baseball.

We are to find the probability that a random student picked plays both tennis and basketball.

Let the total number of students in the school be 100. Also, let T and B represents the set of students who play tennis and basketball respectively.

Then, according to the given information, we have

`n(T)=40,~~~n(B)=24.`

The number of students who play either tennis or basketball will be represented by T ∪ B.

And so, we have

`n(T\cup B)=100-58=42.`

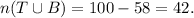
We know that the number of students who play both tennis and basketball is denoted by T ∩ B.

From set theory, we get

`n(T\cup B)=n(T)+n(B)-n(T\cap B)\\\\\Rightarrow n(T\cap B)=n(T)+n(B)-n(T\cup B)\\\\\Rightarrow n(T\cap B)=40+24-42\\\\\Rightarrow n(T\cap B)=22.`

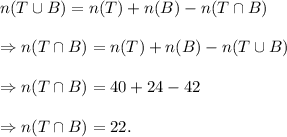
Thus, the required probability that the random student selected plays both tennis and basketball is 22%.