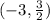Question

Pre-image point N(6, -3) was dilated to point N'(2, -1). What was the scale factor used?

What is the midpoint between (-8, 5) and (2, -2)?

Answer 1

Scale Factor = (-4,2)

Mid-point = (-3, 3/2)

Explanation:

Let X = (x,y) be the scale factor by which the point was dilated. Using this assumption we can write that:

N+X=N^'

(6,-3)+(x,y)=(2,-1)

(6+x,-3+y)=(2,-1)

Putting the coordinates equal one by one:

For x-coordinate:

6+x=2

x=2-6

x= -4

For y-coordinate:

-3+y= -1

y= -1+3

y=2

So the scale factor was:

(-4,2)

For the mid-point of (-8,5) and (2,-2)

Mid-point=((-8+2)/2,(5-2)/2)

=((-6)/2,3/2)

=(-3,3/2)

Answer 2

Question 1

Let the scale factor be k.

Then, we have the mapping

`N(6,-3)\to N'(6k,-3k)`

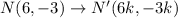
This implies that:

`(6k,-3k)=(2,-1)`

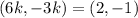
We equate any corresponding component find the value of the scale factor k.

6k=2

`k=(2)/(6)`

`k=(1)/(3)`

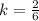
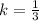
Hence the scale factor is
`(1)/(3)`

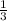
Question 2:

The midpoint of any two points can be calculated using the formula;

`((x_1+x_2)/(2), (y_1+y_2)/(2))`

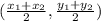
We want to find the midpoint of (-8, 5) and (2, -2).

`((-8+2)/(2), (5+-2)/(2))`

`((-6)/(2), (3)/(2))`

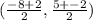
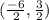
The midpoint is:

`(-3, (3)/(2))`