Answer:
A cone: B. V = 100.48 cubic units
A cylinder: C. V = 301.44 cubic units
Explanation:
The formula of a volume of a cone:
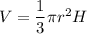
r - radius
H - height
We have r = 4 u and H = 6 u. Substitute:
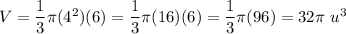
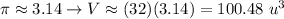
If the cylinder has the same radius and height as a cone, then the volume of the cylinder is three times larger than the volume of the cone.
Therefore, the volume of acylinder:
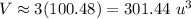
Why?
The formula of a volume of a cone:
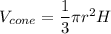
The formula of a volume of a cylinder:
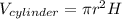
Therefore
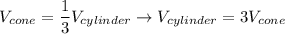
If the radius and height are the same.