Answer: The pressure will also increase 4 times.
Step-by-step explanation:
To calculate the final temperature of the system, we use the equation given by Gay-Lussac Law. This law states that pressure of the gas is directly proportional to the temperature of the gas at constant pressure.
Mathematically,

where,
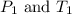 are the initial pressure and temperature of the gas.
are the initial pressure and temperature of the gas.
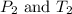 are the final pressure and temperature of the gas.
are the final pressure and temperature of the gas.
We are given:
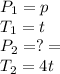
Putting values in above equation, we get:
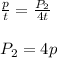
Hence, the pressure will also increase 4 times.