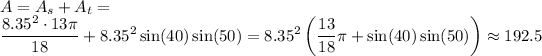The purple area is the sum of the circle sector and the triangle:
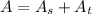
Let's compute them one at the time:
The sector is identified by an angle of 260°, because it is the remainder of a 100° angle.
We can build this simple proportion
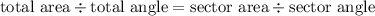
The area of the circle is
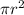 , so we have
, so we have
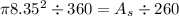
Solving for the sector area, we have
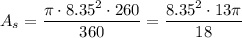
The triangle is an isosceles triangle, because two of the sides are radii. This means that the height is also a bisector, so we can cut the triangle in two 90-50-40 triangles.
Using the law of sines, we can deduce that the height is
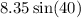
And half the base is
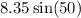
So, the area of the triangle is
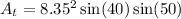
So, the purple area is