∆BOC is equilateral, since both OC and OB are radii of the circle with length 4 cm. Then the angle subtended by the minor arc BC has measure 60°. (Note that OA is also a radius.) AB is a diameter of the circle, so the arc AB subtends an angle measuring 180°. This means the minor arc AC measures 120°.
Since ∆BOC is equilateral, its area is √3/4 (4 cm)² = 4√3 cm². The area of the sector containing ∆BOC is 60/360 = 1/6 the total area of the circle, or π/6 (4 cm)² = 8π/3 cm². Then the area of the shaded segment adjacent to ∆BOC is (8π/3 - 4√3) cm².
∆AOC is isosceles, with vertex angle measuring 120°, so the other two angles measure (180° - 120°)/2 = 30°. Using trigonometry, we find
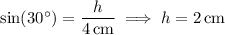
where
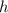 is the length of the altitude originating from vertex O, and so
is the length of the altitude originating from vertex O, and so
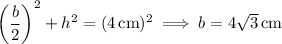
where
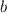 is the length of the base AC. Hence the area of ∆AOC is 1/2 (2 cm) (4√3 cm) = 4√3 cm². The area of the sector containing ∆AOC is 120/360 = 1/3 of the total area of the circle, or π/3 (4 cm)² = 16π/3 cm². Then the area of the other shaded segment is (16π/3 - 4√3) cm².
is the length of the base AC. Hence the area of ∆AOC is 1/2 (2 cm) (4√3 cm) = 4√3 cm². The area of the sector containing ∆AOC is 120/360 = 1/3 of the total area of the circle, or π/3 (4 cm)² = 16π/3 cm². Then the area of the other shaded segment is (16π/3 - 4√3) cm².
So, the total area of the shaded region is
(8π/3 - 4√3) + (16π/3 - 4√3) = (8π - 8√3) cm²