Question

Hi need help thanks!!!!!??????

Answer 1

The slope-intercept form of a line is

`y=mx+q`

where m is the slope and q is the y-intercept. Let's rewrite the equation of the line to match that pattern:

`-3x+4y=-12 \iff 4y = 3x-12 \iff y = (3)/(4)x-3`

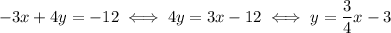
The y intercept tells us that the line passes through the point
`(0,-3)`

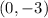
The slope tells us that every time x increases by 1, y increases by 3/4. This is equivalent to say that every time x increases by 4, y increases by 3 (and it's easier to draw).

So, you can start from point
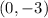`(0,-3)`, and then increase x by 4 and y by 3 to find the next point, which is
`(4,0)`.

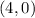Connect the two points, and you'll have the line.