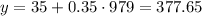Answer:
1. y=0.35x+35
2. If 979 minutes are used, the total cost will be $377.65 dollars.
Explanation:
1. Let $x be the flat monthly fee and $y be the amount of money paid per minute used on the phone.
If a customer uses 210 minutes, the monthly cost will be $108.5, thus
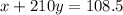
If the customer uses 620 minutes, the monthly cost will be $252, then
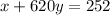
Subtract from the second equation the first one:
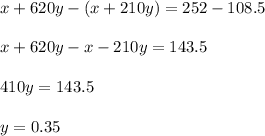
Substitute it into the first equation
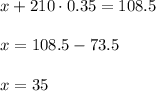
We get the flat fee is $35 and the amount of money per minure used is $0.35. So, the equation of the function is
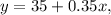
where x is the number of monthly minutes used and y is the total monthly of the NextFell plan.
2. When x=979, then