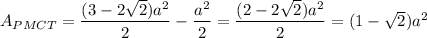Question

Given: PRST is a square

PMKD is a square
PR = a, PD = a
Find the area of PMCT.

Answer 1

`(1-√(2))a^2`

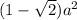
Explanation:

Consider irght triangle PRS. By the Pythagorean theorem,

`PS^2=PR^2+RS^2\\ \\PS^2=a^2+a^2\\ \\PS^2=2a^2\\ \\PS=√(2)a`

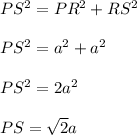
Thus,

`MS=PS-PM=√(2)a-a=(√(2)-1)a`

Consider isosceles triangle MSC. In this triangle

`MS=MC=(√(2)-1)a.`

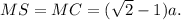
The area of this triangle is

`A_(MSC)=(1)/(2)MS\cdot MC=(1)/(2)\cdot (√(2)-1)a\cdot (√(2)-1)a=((√(2)-1)^2a^2)/(2)=((3-2√(2))a^2)/(2)`

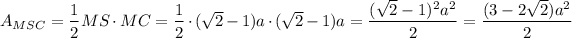
Consider right triangle PTS. The area of this triangle is

`A_(PTS)=(1)/(2)PT\cdot TS=(1)/(2)a\cdot a=(a^2)/(2)`

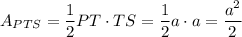
The area of the quadrilateral PMCT is the difference in area of triangles PTS and MSC:

`A_(PMCT)=((3-2√(2))a^2)/(2)-(a^2)/(2)=((2-2√(2))a^2)/(2)=(1-√(2))a^2`