Question

A gas occupies a volume of 180 mL at 35.5°C and 53.9 kPa. What is the volume of gas at STP in mL?

Answer 1

Volume of the gas under STP is 84.7 mL.

Assumption: the gas is ideal.

Step-by-step explanation:

How many moles of particles in this gas?

Convert all units to SI units before applying the ideal gas law.

• The volume shall be in cubic meters:
  `\displaystyle V = \rm 180\;mL * \frac{1\;\text{m}^(3)}{10^(6)\;mL} = 1.80* 10^(-4)\;m^(3)`.
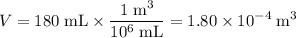• The temperature shall be in degrees Kelvins:
  `T =\rm 35.5\;\textdegree{C} = (35.5 + 273.15)\;K = 308.65\;K`
• The pressure shall be in Pascals:
  `\displaystyle P = \rm 53.9\;kPa * (10^(3)\;Pa)/(1\;kPa) = 5.39* 10^(4)\;Pa`.

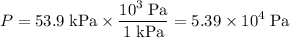The ideal gas constant:
`R \approx \rm 8.314\;Pa\cdot m^(3)\cdot K^(-1)\cdot mol^(-1)`.

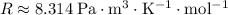The ideal gas law:

`P \cdot V = n \cdot R\cdot T`

Rearrange the ideal gas law to find the number of moles of particles
`n` in this gas:

`\displaystyle n = (P\cdot V)/(R\cdot T) = (5.39* 10^(4)* 1.80* 10^(-4))/(8.314* 308.65) = \rm 3.78081* 10^(-3)\;mol`.

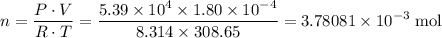The volume of one mole of an ideal gas under STP is 22.4 liters. The volume of
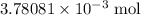`\rm 3.78081* 10^(-3)\;mol` of gas will be:

`\rm 3.78081* 10^(-3)\;mol* 22.4\;L\cdot mol^(-1) = 0.0846901\;L = 84.7\; mL`.

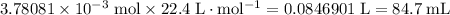All three values in the question come with three significant figures. Keep more significant figures than that in calculations and round the final answer to three significant figures. Hence the answer: 84.7 mL.