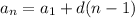Question

If each term of a sequence changes by a common difference,d, what would a general rule for this type of sequence

A.) a(n)=(d)n-1
B.) an=an-1+d
C.) an=an-1+an-2
D.) an=n-1+an-2+d

Answer 1

Answer: Choice B

===================================================

Step-by-step explanation:

The idea is that for any term, we add on the common difference d to get the next term. For example, the sequence {3, 7, 11, 15, 19, 23, ...} has us add on 4 each time so d = 4 in this case.

3+4 = 7

7+4 = 11

11+4 = 15

and so on. The nth term is represented by the notation
`a_n` while the term just before the nth term is written as
`a_(n-1)`

So adding d onto the term just before the nth term gets us the nth term which is how we end up with
`a_n = a_(n-1)+d`

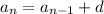
This is the recursive form of the arithmetic sequence. The closed form is written as
`a_n = a_1 + d(n-1)`