Question

What is the simplified form of x plus 4 over x squared minus 3x minus 10⋅x minus 3 over x squared plus x minus 12? (6 points)

1 over the quantity x minus 3 times the quantity x plus 4


1 over the quantity x minus 3 times the quantity x plus 2


1 over the quantity x plus 4 times the quantity x minus 5


1 over the quantity x plus 2 times the quantity x minus 5

Answer 1

The simplified form is 1 over the quantity x plus 2 times the quantity

x minus 5 ⇒ 1/(x+2)(x-5) ⇒ last answer

Explanation:

* Lets write the product of the two fraction

∵
`(x+4)/(x^(2)-3x-10) *(x-3)/(x^(2)+x-12)`

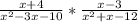
- At first factorize the denominators

# x² - 3x - 10

∵ x² = x × x ⇒ 1st term in the 1st bracket and 1st term in the

2nd bracket

∵ -10 = 2 × -5 ⇒ 2nd term in the 1st bracket and 2nd term in the

2nd bracket

∵ x × - 5 = -5x ⇒ ext-reams

∵ x × 2 = 2x ⇒ means

∵ 2x + -5x = -3x ⇒ middle term

∴ x² - 3x - 10 = (x + 2)(x - 5)

# x² + x - 12

∵ x² = x × x ⇒ 1st term in the 1st bracket and 1st term in the

2nd bracket

∵ -12 = -3 × 4 ⇒ 2nd term in the 1st bracket and 2nd term in the

2nd bracket

∵ x × 4 = 4x ⇒ ext-reams

∵ x × -3 = -3x ⇒ means

∵ 4x + -3x = x ⇒ middle term

∴ x² + x - 12 = (x - 3)(x + 4)

* Lets write the fractions after factorization

∴
`(x+4)/((x+2)(x-5))*(x-3)/((x-3)(x+4))`

- lets simplify the fractions by cancel (x - 3) up with (x - 3) down

and cancel(x + 4) up with (x + 4) down

∴
`(1)/((x+2)(x-5))*1=(1)/((x+2)(x-5))`

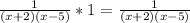
* The simplified form is 1 over the quantity x plus 2 times the

quantity x minus 5