Answer:
Shift to the right 3 units
Explanation:
Translations are a type of rigid transformation of functions, in which the position of the graph of a function is modified. The general form of the graph of a function moves up, down, left, or right.
Vertical translations:
Let:
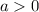
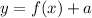 shifts the graph
shifts the graph
 units up
units up
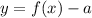 shifts the graph
shifts the graph
 units down
units down
Horizontal translations:
Let:
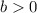
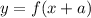 shifts the graph
shifts the graph
 units to the left.
units to the left.
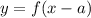 shifts the graph
shifts the graph
 units to the right.
units to the right.
Using the previous information we can conclude that the function:
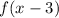
Is a Horizontal translation in which the graph was shifted
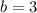 units to the right.
units to the right.
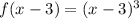
I leave you the graphs, so you can corroborate the answer easily.