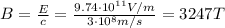Question

Scientists are working on a new technique to kill cancer cells by zapping them with ultrahigh-energy (in the range of 1012 W) pulses of electromagnetic waves that last for an extremely short time (a few nanoseconds). These short pulses scramble the interior of a cell without causing it to explode, as long pulses would do. We can model a typical such cell as a disk 4.0 μm in diameter, with the pulse lasting for 5.0 ns with an average power of 1.59×1012 W . We shall assume that the energy is spread uniformly over the faces of 100 cells for each pulse.a. How much energy is given to the cell during this pulse? U=___Jb. What is the intensity (in W/m^2) delivered tothe cell? I=___W/m^2c. What is the maximum value of the electric field in the pulse?Emax=___V/md. What is the maximum value of the magnetic field in the pulse?Bmax=___T

Answer 1

1.
`7.95\cdot 10^6 J`

The total energy given to the cells during one pulse is given by:

`E=Pt`

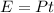
where

P is the average power of the pulse

t is the duration of the pulse

In this problem,

`P=1.59\cdot 10^(12)W`

`t=5.0 ns = 5.0\cdot 10^(-9) s`

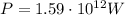
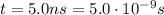
Substituting,

`E=(1.59\cdot 10^(12)W)(5.0 \cdot 10^(-6)s)=7.95\cdot 10^6 J`

2.
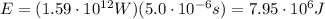
`1.26\cdot 10^(21)W/m^2`

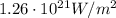
The energy found at point (1) is the energy delivered to 100 cells. The radius of each cell is

`r=(4.0\mu m)/(2)=2.0 \mu m = 2.0\cdot 10^(-6)m`

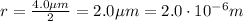
So the area of each cell is

`A=\pi r^2 = \pi (2.0 \cdot 10^(-6)m)^2=1.26\cdot 10^(-11) m^2`

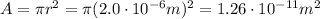
The energy is spread over 100 cells, so the total area of the cells is

`A=100 (1.26\cdot 10^(-11) m^2)=1.26\cdot 10^(-9) m^2`

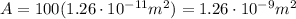
And so the intensity delivered is

`I=(P)/(A)=(1.59\cdot 10^(12)W)/(1.26\cdot 10^(-9) m^2)=1.26\cdot 10^(21)W/m^2`

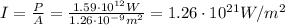
3.
`9.74\cdot 10^(11) V/m`

The average intensity of an electromagnetic wave is related to the maximum value of the electric field by

`I=(1)/(2)c\epsilon_0 E^2`

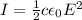
where

c is the speed of light

`\epsilon_0` is the vacuum permittivity

E is the amplitude of the electric field

Solving the formula for E, we find:

`E=\sqrt{(2I)/(c\epsilon_0)}=\sqrt{(2(1.26\cdot 10^(21) W/m^2))/((3\cdot 10^8 m/s)(8.85\cdot 10^(-12)F/m))}=9.74\cdot 10^(11) V/m`

4. 3247 T

The magnetic field amplitude is related to the electric field amplitude by

`E=cB`

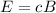
where

E is the electric field amplitude

c is the speed of light

B is the magnetic field

Solving the equation for B and substituting the value of E that we found at point 3, we find

`B=(E)/(c)=(9.74\cdot 10^(11) V/m)/(3\cdot 10^8 m/s)=3247 T`