Answer: Option b
b. x greater or equal than 1.8
Explanation:
In this problem we have the following inequality:

To solve it we must group the x on one side and the constants on the other side

Apply distributive property on the right side of the inequality

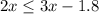
Subtract 3x on both sides of the inequality
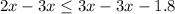
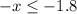
Multiply by -1 both sides of the inequality
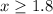
The answer is the option b