Question

A pendulum has 532 J of potential energy at the highest point of its swing. How much kinetic energy will it have at the bottom of its swing?

Answer 1

532 J

Step-by-step explanation:

If there are no frictional forces/air resistance involved in the problem, then the mechanical energy of the system is conserved.

This means that:

`E_i = E_f`

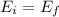
where E_i is the initial mechanical energy and E_f is the final mechanical energy. The mechanical energy is the sum of potential energy U and kinetic energy K:

`U_i + K_i = U_f + K_f`

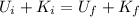
At the highest point, the speed of the swing is zero, so

`K_i = 0`

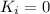
while at the bottom point, the potential energy is zero (if we take the bottom point of the swing as reference level), so

`U_f =0`

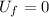
This means that the previous equation becomes

`U_i = K_f`

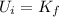
and since

`U_i = 532 J`

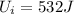
the kinetic energy at the bottom of its swing is

`K_f = 532 J`