Question

Given: △EIJ, k(O, r)
EI = EJ = r=10 cm
EP ⊥ IJ
Find: JP

Answer 1

`JP=5√(3)\ cm`

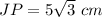
Explanation:

Connecting points O and E and points O and J, we get triangle EOJ. This triangle is equilateral triangle, because OJ=OE=JE=r=10 cm.

Since EP⊥IJ, then segment JP is the height of the triangle EOJ.

The height of the equilateral triangle can be found using formula

`h=(a√(3))/(2),`

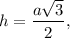
where a is the side length.

So,

`h=(10√(3))/(2)=5√(3)\ cm.`