Answer:
The measure of angles of △SPT are
∠PTS=35°, ∠PST=19°, ∠SPT=126°
Explanation:
Given the figure in which
m∠EPT=54° and arc TP=70°
we have to find angles of △SPT
By tangent chord angle theorem, which states that the angle make by a tangent to a circle and a chord is equals to half of the angle measure of the intercepted arc i.e
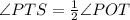
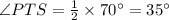
As ∠EPT and ∠SPT form linear pair therefore their sum equals to 180°
⇒ ∠EPT+∠SPT=180°
54°+∠SPT=180°
∠SPT=126°
In △SPT, by angle sum property of triangle
∠PST+∠SPT+∠PTS=180°
∠PST+126°+35°=180°
∠PST=19°