Question

Which of the following is a valid comparison between the possible minimum and maximum values of the function y = -x2 + 4x - 8 and the graph below?

The maximum value of the equation is 1 less than the maximum value of the graph.
The minimum value of the equation is 1 less than the minimum value of the graph.
The minimum value of the equation is 1 greater than the minimum value of the graph.
The maximum value of the equation is 1 greater than the maximum value of the graph.

Answer 1

The maximum value of the equation is 1 less than the maximum value of the graph

Explanation:

Answer 2

The maximum value of the equation is 1 less than the maximum value of the graph

Explanation:

We have the equation
`y=-x^2+4x-8`.

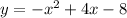We can know that this graph will have a maximum value as this is a negative parabola.

In order to find the maximum value, we can use the equation
`x=(-b)/(2a)`

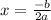
In our given equation:

a=-1

b=4

c=-8

Now we can plug in these values to the equation

`x=(-4)/(-2) \\\\x=2`

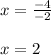
Now we can plug the x value where the maximum occurs to find the max value of the equation

`y=-(2)^2+4(2)-8\\\\y=-4+8-8\\\\y=-4`

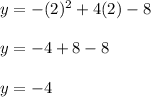
This means that the maximum of this equation is -4.

The maximum of the graph is shown to be -3

This means that the maximum value of the equation is 1 less than the maximum value of the graph