Question

Which statement BEST describes how the graph of g(x)=−5x^2 compares to the graph off(x)=x^2? Question 11 options:

A)The graph of g(x) is a vertical stretch of f(x) by a factor of 5.
B) The graph of g(x) is a reflection of f(x) across the x-axis.
C)The graph of g(x) is a vertical compression of f(x) by a factor of 15 and reflection across the x-axis.
D) The graph of g(x) is a vertical stretch of f(x) by a factor of 5 and a reflection across the x-axis.

Answer 1

D) The graph of g(x) is a vertical stretch of f(x) by a factor of 5 and a reflection across the x-axis

Explanation:

I just did this and got it correct

Answer 2

D) The graph of g(x) is a vertical stretch of f(x) by a factor of 5 and a reflection across the x-axis

Explanation:

The functions
`f(x)=x^2` is called the base function for the vertical parabola.

If this function is reflected across the x-axis, the parent function is negated to get the transformed function, which is
`h(x)=-x^2`

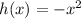
If the resulting function is stretched vertically by a factor of 5, we multiply it by 5 to get;

`g(x)=-5x^2`

The correct choice is D.