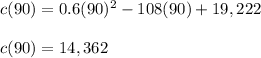Question

A medical equipment industry manufactures X-ray machines. The unit cost c

(the cost in dollars to make each X-ray machine) depends on the number of machines made. If x machines are made, then the unit cost is given by the function
c(x)=0.6x^2-108x+19,222. What is the minimum unit cost?

Do not round your answer

Answer 1

The minimum unit cost is 14,362

Explanation:

The minimum unit cost is given by a quadratic equation. Therefore the minimum value is at its vertex

For a quadratic function of the form

`ax ^ 2 + bx + c`

the x coordinate of the vertex is

`x=-(b)/(2a)`

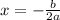
In this case the equation is:
`c(x) = 0.6x^2-108x+19,222`

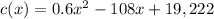
Then

`a= 0.6\\b=-108\\c=19,222`

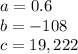
Therefore the x coordinate of the vertex is:

`x=-((-108))/(2(0.6))`

`x=90`

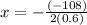
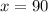
Finally the minimum unit cost is:

`c(90)=0.6(90)^2-108(90)+19,222\\\\c(90)=14,362`

Answer 2

Minimum Unit Cost = $14,362

Explanation:

The standard form of a quadratic is given by:

ax^2 + bx + c

So for our function, we can say,

a = 0.6

b = -108

c = 19,222

We can find the vertex (x-coordinate where minimum value occurs) by the formula -b/2a

So,

-(-108)/2(0.6) = 108/1.2 = 90

Plugging this value into original function would give us the minimum (unit cost):

`c(x)=0.6x^2-108x+19,222\\c(90)=0.6(90)^2-108(90)+19,222\\=14,362`