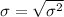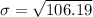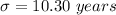Question

Ten people at a party decide to compare ages. Five people are 30 years old, three are 32, one is 31, and one is 65.

Given the ages of the ten people, to the nearest tenth, determine the average of their ages and the standard deviation.

A. The mean age of the ten people at a party is

B. The standard deviation is:

Answer 1

A. The mean age of the ten people at a party is 34.2 years

B. The standard deviation is 10.30 years

Explanation:

The average of the ages of the people is defined as:

`{\displaystyle {\overline {x}}} =(\sum^n_i x_i)/(n)`

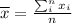
Where
`x_1, x_2\ ,...,\ x_n` are the ages of the people and n is the number of people

Then

`n=10`

`{\overline {x}}} =(5*30 + 3*32 + 31 + 65)/(10)\\\\{\overline {x}}}=34.2\ years`

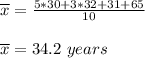
To calculate the standard deviation we calculate the squared differences between the mean and
`x_i`

`5*(34.2 - 30)^2 = 88.2\\\\3*(34.2-32)^2 = 14.52\\\\(34.2-31)^2 = 10.24\\\\(34.2 - 65)^2 = 948.64`

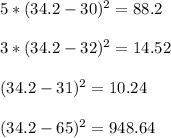
Now we add the differences and divide them by the total number of people and we get the variance

`\sigma^2=(88.2+14.52+10.54+948.64)/(10)=106.19`

Finally the standard deviation is

`\sigma=√(\sigma^2)`

`\sigma= √(106.19)`

`\sigma=10.30\ years`