Answer:
Option B is correct answer.
Explanation:
We need to solve the expression sec2xcot2x.
We know sec x = 1/ cos x and cot x = 1/ tan x and tan x = sin x/cos x and 1/tanx = cosx /sinx
Since in question we 2x instead of x so, replacing x with 2x and Putting values:
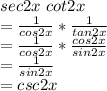
So, Option B is correct answer.