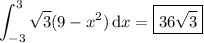Recall that the area of an equilateral triangle with side length
 is
is
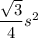 .
.
In the
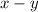 plane, the base is given by two equations:
plane, the base is given by two equations:
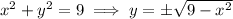
so that for any given
 , the vertical distance between the two sides of the circle is
, the vertical distance between the two sides of the circle is
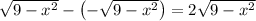
and this is the side of length of each triangular cross-section for each
 . Then the area of each cross-section is
. Then the area of each cross-section is
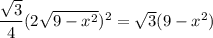
and the volume of the solid is