Question

How many 5-digit numbers can be created

using the digits 2, 3, 5, 7, and 8 without
repeating any digits within that 5-digit
number?

Answer 1

120.

Explanation:

That would be factorial 5, written 5!.

That is 5*4*3*2*1

= 120.

Answer 2

120

Explanation:

We have 5 digits that can be used to create different 5 digit numbers. We are also not allowed to repeat any numbers. Let's say we have 5 boxes to put the 5 numbers in.

Box 1

Box 2

Box 3

Box 4

Box 5

In the first box, we have 5 different choices. Since we aren't allowed to repeat any digits, the second box only has 4 different choices. And so on...

Box 1 --> 5 choices

Box 2 --> 4 choices

Box 3 --> 3 choices

Box 4 --> 2 choices

Box 5 --> 1 choice

Therefore the amount of 5 digit numbers that can be created is:

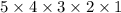`5*4*3*2*1` or 5 factorial (a factorial is all the product of all the positive integers equal to and less than the number), which is equivalent to:

120 5-digit numbers