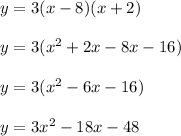Question

Which equation when graphed has X-intercepts at (8,0) and (-2, 0) and a y-intercept at (0-48)?

Answer 1

Answer: fx=3(x-8)(x+2) or answer C

Explanation:

bc i said so

Answer 2

`y=3x^(2)-18x-48`

Explanation:

we know that

The equation of a vertical parabola in factored form is equal to

`y=a(x-x1)(x-x2)`

where

a is a coefficient

x1 an x2 are the roots or x-intercepts

In this problem we have

`x1=8,x2=-2`

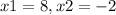
substitute

`y=a(x-8)(x+2)`

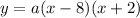
with the y-intercept (0,-48) find the value of a

substitute

`-48=a(0-8)(0+2)`

`-48=-16a`

`a=3`

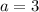
The equation is equal to

`y=3(x-8)(x+2)\\ \\y=3(x^(2)+2x-8x-16)\\ \\ y=3(x^(2) -6x-16)\\ \\y=3x^(2)-18x-48`