Question

Two small identical conducting spheres are placed with their centers 0.41 m apart. One is given a charge of 12 ✕ 10−9 C, the other a charge of −23 ✕ 10−9 C. (a) Find the electrostatic force exerted on one sphere by the other. magnitude 1.48e-5 Correct: Your answer is correct. N direction attractive Correct: Your answer is correct. (b) The spheres are connected by a conducting wire. Find the electrostatic force between the two after equilibrium is reached, where both spheres have the same charge.

Answer 1

The final charge on each sphere after contact will be −4 nC, which reflects the even distribution of the combined charges initially present on both spheres.

Step-by-step explanation:

When two charged metal conducting spheres are brought into contact, their charges redistribute evenly between them because they are identical. This is because the total charge is conserved, and it will be shared equally when the two spheres touch.

If sphere A has a charge of −5 nC (nanoCoulombs) and sphere B has a charge of −3 nC, after they touch, they will both have the same charge. We calculate the final charge on each by adding the charges together and then dividing by two, which gives us (−5 nC + −3 nC)/2 = −4 nC on each sphere. The −4 nC corresponds to a specific number of electrons, where the charge of one electron is ≎1.6×10−19 C.

Answer 2

(a)
`-1.48\cdot 10^(-5)N`

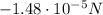
The electrostatic force exerted between the two sphere is given by:

`F=k(q_1 q_2)/(r^2)`

where

k is the Coulomb's constant

q1, q2 are the charges on the two spheres

r is the separation between the centres of the two spheres

In this problem,

`q_1 = 12\cdot 10^(-9) C\\q_2 = -23\cdot 10^(-9) C\\r = 0.41 m`

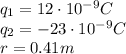
Substituting these values into the equation, we find the force

`F=(9\cdot 10^9 Nm^2 C^(-2) )((12\cdot 10^(-9)C)(-23\cdot 10^(-9) C))/((0.41 m)^2)=-1.48\cdot 10^(-5)N`

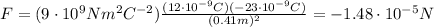
And the negative sign means the force is attractive, since the two spheres have charges of opposite sign.

(b)
`+1.62\cdot 10^(-6)N`

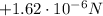
The total net charge over the two sphere is:

`Q=q_1 +q_2 = 12\cdot 10^(-9)C+(-23\cdot 10^(-9)C)=-11\cdot 10^(-9) C`

When the two spheres are connected, the charge distribute equally over the two spheres (since they are identical, they have same capacitance), so each sphere will have a charge of

`q=(Q)/(2)=(-11\cdot 10^(-9)C)/(2)=-5.5\cdot 10^(-9)C`

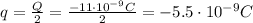
So the electrostatic force between the two spheres will now be

`F=k(q^2)/(r^2)`

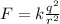
And substituting numbers, we find

`F=(9\cdot 10^9 Nm^2 C^(-2) )((-5.5\cdot 10^(-9) C)^2)/((0.41 m)^2)=+1.62\cdot 10^(-6)N`

and the positive sign means the force is repulsive, since the two spheres have same sign charges.