Question

What value for c will make the expression a perfect square trinomial? x2 – 7x + c

Answer 1

D.
`(49)/(4)`.

Explanation:

We have been given a trinomial
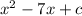`x^2-7x+c`. We are asked to find the value of c, which will make the expression a perfect square trinomial.

We know that a perfect trinomial is in form
`a^2\pm2ab+b^2`.

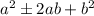We will use complete the square process to solve for c.

To complete a square, we need to add square of half the coefficient of x term. We can see that coefficient of x is -7, so the value of c would be:

`((b)/(2))^2=((-7)/(2))^2=((-7)^2)/(2^2)=(49)/(4)`.

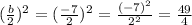Therefore, the value of c required to make the given expression a perfect trinomial is
`(49)/(4)` and option D is the correct choice.

Answer 2

Final answer is
`(49)/(4)`.

Explanation:

Given expression is
`x^2-7x+c`.

Now we need to find about what value for c will make the given expression
`x^2-7x+c`, a perfect square trinominal.

Coefficient of middle term that contains x, in
`x^2-7x+c` -7.

Take half of that so we get
`-(7)/(2)`.

Then take square of the half value.

We get
`\left(-(7)/(2)\right)^2=(49)/(4)`.

We add the square value to make perfect square trinomial.

Hence final answer is
`(49)/(4)`.