Question

Im not sure how to find the missing angle

Answer 1

Explanation:

the question is asking for the length of the side labeled x

use Pythagoras' theorem to find that side

where c = x because c represents the hypotenuse in the theorem and x is on the hypotenuse in this problem

c =
`\sqrt{a^(2) + b^(2) }`

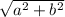
sooo plug in a = 14 and b = 10

c =
`\sqrt{14^(2) + 10^(2) }`

c =
`√(196+100)`

c =
`√(296)`

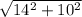
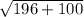
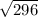
c= 17.20465..... ( that's the approx. length of side x in the problem )

since this is a right triangle we could use trigonometry to find the two angles use SOH CAH TOA to remember how those functions fit on the triangle.

Sin(Ф)=Opp/Hyp Cos(Ф)=Adj/Hyp Tan(Ф)=Opp/Adj

since we know the Hyp (hypotenuse) and the side adjacent will be the side with the 10 soooo...

Cos(Ф)=10/17.20465

Ф = arcCos(10/17.20465)

Ф = 54.4623° is the angle on the side with 10

the side with 14 then has an angle of 35.5376°

:)