Answer:
Each donut costs $2 and each cookie costs $1.5
Explanation:
1. Let´s name the variables as the following:
x = price of one donut
y = price of one cookie
2. Write in an equation form which Bentley bought:
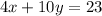 (Eq.1)
(Eq.1)
3. Write in an equation form which Skylar bought:
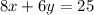 (Eq.2)
(Eq.2)
4. Solve for x in Eq.1:
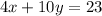

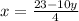 (Eq.3)
(Eq.3)
5. Replace Eq.3 in Eq.2 and solve for y:
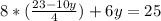
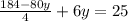
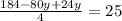

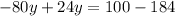
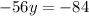
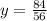
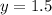
6. Replacing the value of y in Eq.3:
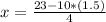
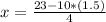
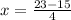
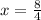

Therefore each donut costs $2 and each cookie costs $1.5