The inverse of the function f(x) = 3x + 5 is
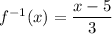
How to determine the inverse of the function
From the question, we have the following parameters that can be used in our computation:
f(x) = 3x + 5
Express the function as an equation
So, we have
y = 3x + 5
Swap the occurrence of x and y in the equation
This gives
x = 3y + 5
Subtract 5 from all sides
3y = x - 5
So, we have
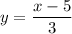
Express as an inverse function
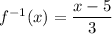
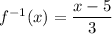
Verifying the relationship
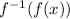 and
and
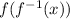
We have
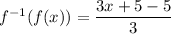
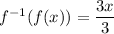
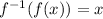
Also, we have
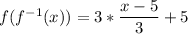
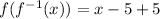
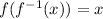
Hence, the inverse of the function is
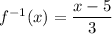
Question
Find the inverse of the function below and write it in the form y = f^-1(x)
Verify the relationshipsf(f^-1(x)) and f^-1(f(x))=x
f(x)=3x+5