Question

A road has a 10% grade, meaning increasing 1 unit of rise to every 10 units of run.

a) What is the elevation of the road to the nearest degree?

b) If the road is two km long, how much does it rise? Round your answer to the nearest tenth?

Answer 1

The grade is the ratio of rise to run, i.e. the slope aka the tangent.

`\tan \theta = (1)/(10)`

`\theta = \arctan 0.1 \approx 5.711^\circ`

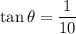
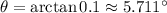
Answer: (a) 6 degrees

For part b, the road is the hypotenuse c of a right triangle whose tangent of the small angle is 1/10. The height h or rise is the side opposite the small angle.

`\sin\theta = \frac h c`

`h = c \sin \theta`

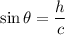
We could just take the sine of the angle we got but let's get it from the tangent exactly.

`\cos^2 \theta + \sin ^2 \theta = 1`

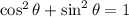
Dividing by squared cosine

`1 + \tan ^2 \theta = 1/\cos^2 \theta = 1/(1- \sin^2 \theta)`

`(1- \sin^2 \theta) = 1/(1 + \tan^2 \theta)`

`\sin^2 \theta = 1 - 1/(1 + \tan^2 \theta)`

`\sin^2 \theta = 1 - 1/(1 + (1/10)^2) = 1-1/(101/100) = 1/101`

`h = c \sin \theta = 2 √(1/101) \approx 0.199`

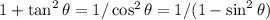
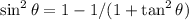
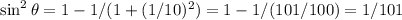
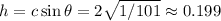
Answer: (b) Rise of 0.199 km