The axis of symmetry of a parabola like

is a vertical line of the form
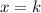
where k is the x coordinate of the vertex of the parabola.
In particular, the x coordinate of the vertex of the parabola is given by
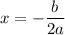
which in your case becomes
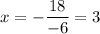
So, the axis of symmetry is the line
