Answer:
The value of x is 24.
Explanation:
Given information: In ΔGHE, ED is angle bisector, EG=44.8 millimeters, GD=(x+4) millimeters, DH=35 millimeters, and EH=56 millimeters.
According to the angle bisector theorem, an angle bisector divide the opposite side into two segments that are proportional to the other two sides of the triangle.
In ΔGHE, ED is angle bisector, By using angle bisector theorem, we get
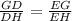
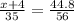
Multiply both the sides by 35.
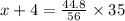
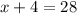
Subtract 4 from both the sides.
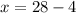
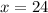
Therefore the value of x is 24.