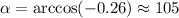If vector 1=(2,5) and vector 2=(4,-3), what is the angle between the two vectors? Round your answer to one decimal place.

Question

asked Feb 28, 2020 24.2k views

1 Answer

Jingqiang Zhang · Answer 1 · 2020-03-05T19:44:29+0000

The dot product between two vectors is defined as

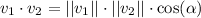
$v_1\cdot v_2 = ||v_1||\cdot ||v_2||\cdot \cos(\alpha)$

where
$\alpha$ is the angle between the two vectors.

So, we deduce

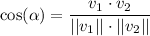
$\cos(\alpha) = (v_1\cdot v_2)/(||v_1||\cdot ||v_2||)$

The dot product is computed as the sum of the product of correspondent coordinates:

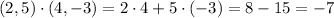
$(2,5)\cdot(4,-3) = 2\cdot 4 + 5\cdot(-3) = 8-15 = -7$

whereas the norm of a vector is the square root of the sum of the squares of the coordinates:

$||v_1|| = √(2^2+5^2)=√(29),\quad ||v_1|| = √(4^2+(-3)^2)=5$

So, we have

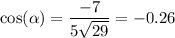
$\cos(\alpha) = (-7)/(5√(29)) = -0.26$

This implies

$\alpha = \arccos(-0.26) \approx 105$