Question

Without graphing predict weather the function y= (1/2)x shows exponential growth or decay. Justify your predictions

Answer 1

The base of the exponential function is 0.5 which is between 0 and 1 and thus this is an exponential decay function.

Explanation:

Exponential equations are usually in the form;

`y=ab^(x)`

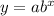
where;

a is the initial value, that is the value of y when x is 0,

b is the growth or decay factor and also the base of the exponential function

If b>1, then it is an exponential growth function and the values of y keep getting bigger.

if 0<b<1, then it is an exponential decay function and the y values keep getting smaller as x increases.

In the function given;

`y=((1)/(2))^(x)`

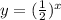
The base of the exponential function is 0.5 which is between 0 and 1 and thus this is an exponential decay function.

In order to justify our prediction, we can simply obtain the graph of the function and check on how x and y vary.

From the attachment below we can see that the values of y become increasingly smaller as the values of x increases in magnitude which justifies our predictions.