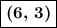Question

Samara is adjusting a satellite because she finds it is not focusing the income radio waves perfectly. The shape of her satellite can be modeled by (y-3)^2 = 8(x-4) where x and y are modeled in inches. She realizes that the static is a result of the feed antenna shifting slightly off the focus point. What is the focus point of the satellite? (-3,-6) (-3,-4) (3,6) 6,3)

Answer 1

`\boxed{\text{(6, 3)}}`

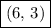
Explanation:

The conic form of the equation for a sideways parabola is

(y - k)² = 4p(x - h)

The focus is at (h + p, k)

The equation of Samara's parabola is

(y - 3)² = 8(x - 4)

h = 4

p = 8/4 = 2

k = 3

h + p = 6

So, the focus point of the satellite dish is at

`\boxed{\textbf{(6, 3)}}`