Question

??anybody help please

Answer 1

a)
`20m+65=28m+25`

b) On the 5th month, the gym will have the same total cost of $165

Explanation:

We can write the following expression for Gym A:

`20m+65`

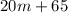
And we can write the following expression for Gym B:

`0.8(35m)+25`

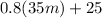
This can we rewritten as

`28m+25`

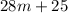
In order to find the total costs at which the gyms are the same, we must set them equal to each other, solve for m, and then substitute m into the equation.

`20m+65=28m+25\\\\8m=40\\\\m=5`

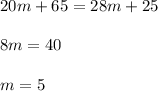
Now we can substitute m into each equation

`20m+65=28m[tex]20(5)+65=28(5)+25\\\\100+65=140+25\\165=165`

On the 5th month, the gym will have the same total cost of $165