Answer:
(n -13)/(n -7)
Explanation:
Simplify the fraction on the left, then add the two fractions.
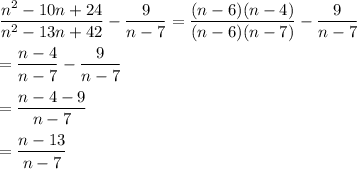
_____
Comment on the graph
The vertical asymptote tells you the simplified form has one zero in the denominator at x=7. That is, the denominator is x-7.
The x-intercept at 13 tells you that x-13 is a factor of the numerator.
The horizontal asymptote at y=1 tells you there is no vertical scaling, so the simplest form is ...
(n -13)/(n -7)
The hole at x=6 is a result of the factor (x-6) that is cancelled from the first fraction in the original expression. At that value of x, the fraction is undefined. So, the above solution should come with the restriction x ≠ 6.