Question

You need 20 liters of 20% acid solution. You have jugs of 10% solution and 25% solution. How many liters of each should you combine to get the needed solution?

Answer 1

6.(6) and 13.(3) liters.

Step-by-step explanation (this way is not the shortest one):

1. the basic rule is: the mas/volume of pure substance after and before combination is the same.

2. There is 4 liters of pure substance in 20*0.2 acid solution (20*0.2=4);

3. if 'x' is the volume of pure substance in 10%-solution; and if 'y' is the volume of pure substance in 20%-solution, then their sum of volumes is 4. It means, x+y=4 - this is the 1-st equation for system.

4. the volume of 10%-solution is x/0.1=10x; the volume of 20%-solution is y/0.25=4y; their sum is 20 litres. It means, 10x+4y=20 - this is the 2-d equation of the system.

5. to calculate the volumes of the pure substance:

`\left \{ {{x+y=4} \atop {10x+4y=20}} \right.  \ =>\ \left \{ {{x=(2)/(3) } \atop {y=(10)/(3) }} \right.`

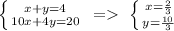
6. to calculate the volume of 10%-solution: 2/3 *10=20/3≈6.(6) litres;

to calculate the volume of 25%-solution: 10/3 *4=40/3≈13.(3) litres.