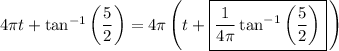Expanding the desired form, we have
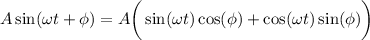
and matching it up with the given expression, we see that
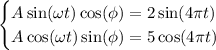
A natural choice for one of the symbols is
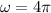 . Then
. Then
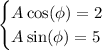
Use the Pythagorean identity to eliminate
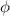 .
.
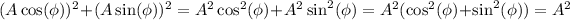
so that
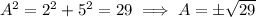
Use the definition of tangent to eliminate
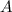 .
.
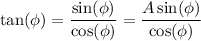
so that
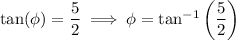
We end up with
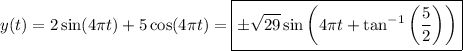
where
• amplitude:
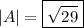
• angular frequency:
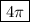
• phase shift: