Question

Model each problem as an equation, and then match to its solution.

Answer 1

Part 1) The larger integer is 11

Part 2) The denominator is 5

Part 3) The positive integer is 4

The graph in the attached figure

Explanation:

Part 1)

Let

x----> the smaller positive integer

y-----> the larger positive integer

we know that

`x^(2) +y^(2) =185` -----> equation A

`x=y-3` -----> equation B

substitute equation B in equation A and solve for y

`(y-3)^(2) +y^(2) =185\\ \\y^(2) -6y+9+y^(2)=185\\ \\2y^(2)-6y-176=0`

using a graphing calculator-----> solve the quadratic equation

The solution is y=11

`x=11-3=8`

Part 2)

Let

x----> the numerator of the fraction

y-----> the denominator of the fraction

we know that

`x=2y+1` ----> equation A

`(x+4)/(y+4)=(5)/(3)` ----> equation B

substitute equation A in equation B and solve for y

`(2y+1+4)/(y+4)=(5)/(3)`

`(2y+5)/(y+4)=(5)/(3)\\ \\6y+15=5y+20\\ \\6y-5y=20-15\\ \\y=5`

`x=2(5)+1=11`

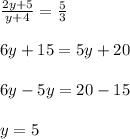
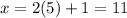
Part 3)

Let

x----> the positive integer

we know that

`x-(1)/(x)=(15)/(4)`

solve for x

`x-(1)/(x)=(15)/(4)\\ \\4x^(2)-4=15x\\ \\4x^(2)-15x-4=0`

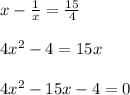
using a graphing calculator-----> solve the quadratic equation

The solution is x=4