Answer:
The required functions are
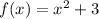 ,
,
 ,
,
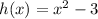 and
and
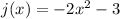 .
.
Explanation:
The vertex from of a parabola is

Where, (h,k) is the vertex of parabola is a is the vertical stretch factor.
If a is negative, then it is downward parabola and if a is positive then it is an upward parabola.
If |a|<1, then it is compressed vertical and if |a|>1, then it is stretched vertically.
The graph of f(x) has vertex at (0,3) and it is not stretch vertically so the value of a is 1. So, the function f(x) is defined as
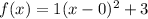
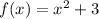
The graph of g(x) has vertex at (0,-3) and it is stretch vertically by factor 2 so the value of a is 2. So, the function g(x) is defined as


The graph of h(x) has vertex at (0,-3) and it is not stretch vertically so the value of a is 1. So, the function h(x) is defined as
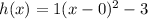
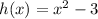
The graph of j(x) has vertex at (0,-3) and it is stretch vertically by factor 2 and it is downward so the value of a is -2. So, the function j(x) is defined as
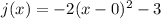
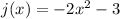
Therefore the required functions are
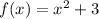 ,
,
 ,
,
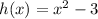 and
and
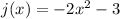 .
.